Finite DMRG algorithm for the Heisenberg chain¶

The goal of this exercise is to implement the finite version of the DMRG algorithm for the antiferromagnetic Heisenberg chain of spins one-half.

The Hamiltonian that we will build is the antiferromagnetic Heisenberg model:

$H=\sum_{i}\vec{S}_{i}\cdot\vec{S}_{i+1}= \sum_{i}\left[S^{z}_{i}S^{z}_{i+1}+ \frac{1}{2}\left(S^{\dagger}_{i}S^{-}_{i+1}+ S^{-}_{i}S^{\dagger}_{i+1}\right)\right]$

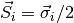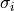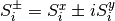where $\vec{S}_{i}=\vec{\sigma}_{i}/2$ are the spin operators, $\sigma_{i}$ are the Pauli matrices, and $S^{\pm}_{i}=S^{x}_{i}\pm i S^{y}_{i}$ .

Exercise¶

Calculate the ground state energy of the antiferromagnetic Heisenberg model for a chain of spins 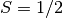$S=1/2$ using the finite version of the DMRG algorithm. You should be able to pass the number of sites of the chain, the number of states kept during the DMRG truncation, and the number of sweeps during the finite algorithm as parameters. The output should be the energy per site, entanglement entropy and, truncation error at each step of the algorithm. You could:

make a plot of the energy per site versus system size to see how converges. The relative error in energy is given by the truncation error. In a given sweep, where is the energy best approximate to the actual value?
for the same size you chose in the last exercise, repeat the same extrapolation for the energy to zero truncation error. Compare this with the exact value for a finite size given by the Bethe Anstatz, and with the results you
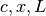find the scaling of the entanglement entropy for the Heisenberg model. The entanglement entropy for open boundary conditions scales as $S(x)=\frac{c}{6}\log\left[\frac{2L}{\pi}sin\left(\frac{\pi x}{L}\right)\right]$ , where $c, x, L$ are the central charge of the model; the size of the part of the chain you keep in the reduced density matrix, and the size of the whole chain, respectively.

Solution¶

This is the first implementation of a full DMRG algorithm in the tutorial. The full DMRG algorithm involves doing first the infinite version of the DMRG algorithm, which we cover in the last exercise, and then a number of sweeps keeping the size of the system fixed. The latter are called finite algorithm sweeps. During the finite sweeps, one block is growing exactly as during the infinite version of the algorithm, while the other has to shrink to keep the system size constant. As the truncation in DMRG can take you only for larger block sizes, you have to use an old version of the block that is shrinking. This is done saving each of the block when they grow, so you simply pull the right one from a list of old blocks.

To being able to reuse this code latter we are going to put all the stuff related to the AF Heisenberg model in a new object. In this way it’s easier to switch between different models. This bring nothing new to the algorithm itself. The file with the model is something like this:

"""A few convenience functions to setup the Heisenberg model.

.. math::
    H=\sum_{i}\vec{S}_{i}\cdot\vec{S}_{i+1}=
    \sum_{i}\left[S^{z}_{i}S^{z}_{i+1}+
    \frac{1}{2}\left(S^{\dagger}_{i}S^{-}_{i+1}+
    S^{-}_{i}S^{\dagger}_{i+1}\right)\right]

"""
class HeisenbergModel(object):
    """Implements a few convenience functions for AF Heisenberg.
    
    Does exactly that.
    """
    def __init__(self):
        super(HeisenbergModel, self).__init__()
		
    def set_hamiltonian(self, system):
        """Sets a system Hamiltonian to the AF Heisenberg Hamiltonian.
    
        Does exactly this. If the system hamiltonian has some other terms on
        it, there are not touched. So be sure to use this function only in
        newly created `System` objects.
    
        Parameters
        ----------
        system : a System.
            The System you want to set the Hamiltonain for.
        """
        system.clear_hamiltonian()
        if 'bh' in system.left_block.operators.keys():
            system.add_to_hamiltonian(left_block_op='bh')
        if 'bh' in system.right_block.operators.keys():
            system.add_to_hamiltonian(right_block_op='bh')
        system.add_to_hamiltonian('id', 'id', 's_z', 's_z')
        system.add_to_hamiltonian('id', 'id', 's_p', 's_m', .5)
        system.add_to_hamiltonian('id', 'id', 's_m', 's_p', .5)
        system.add_to_hamiltonian('id', 's_z', 's_z', 'id')
        system.add_to_hamiltonian('id', 's_p', 's_m', 'id', .5)
        system.add_to_hamiltonian('id', 's_m', 's_p', 'id', .5)
        system.add_to_hamiltonian('s_z', 's_z', 'id', 'id')
        system.add_to_hamiltonian('s_p', 's_m', 'id', 'id', .5)
        system.add_to_hamiltonian('s_m', 's_p', 'id', 'id', .5)
    
    def set_block_hamiltonian(self, tmp_matrix_for_bh, system):
        """Sets the block Hamiltonian to be what you need for AF Heisenberg.
    
        Parameters
        ----------
	tmp_matrix_for_bh : a numpy array of ndim = 2.
	    An auxiliary matrix to keep track of the result.
        system : a System.
            The System you want to set the Hamiltonian for.
        """
        # If you have a block hamiltonian in your block, add it
        if 'bh' in system.growing_block.operators.keys():
            system.add_to_block_hamiltonian(tmp_matrix_for_bh, 'bh', 'id')
        system.add_to_block_hamiltonian(tmp_matrix_for_bh, 's_z', 's_z')
        system.add_to_block_hamiltonian(tmp_matrix_for_bh, 's_p', 's_m', .5)
        system.add_to_block_hamiltonian(tmp_matrix_for_bh, 's_m', 's_p', .5)
    
    def set_operators_to_update(self, system):
        """Sets the operators to update to be what you need to AF Heisenberg.
    
        Parameters
        ----------
        system : a System.
            The System you want to set the Hamiltonian for.

	Notes
	-----
	The block Hamiltonian, althought needs to be updated, is treated
	separately by the very functions in the `System` class.
        """
        system.add_to_operators_to_update('s_z', site_op='s_z')
        system.add_to_operators_to_update('s_p', site_op='s_p')
        system.add_to_operators_to_update('s_m', site_op='s_m')

The real changes are in the functions to grow the blocks, and perform the infinite and finite DMRG steps. As was said above these functions are included not in the main file, as in the previous exercise, but in the System class. Apart from the minor changes introduced by this change in the interface, you show pay attention to the changes in the functions themselves.

The first change we will make is to grow the system asymmetrically. This means that during the infinite version of the algorithm we keep on block (the right one) one-site long. You do this simply but not growing the right block:

Next thing is to write the function to implement the DMRG step during the finite algorithm. The only difference with the infinite version is that now in addition to grow one of the blocks, you set the other one to be the one with the proper size in a previous sweep.

During the finite sweeps you want to increase the number of states that you keep. A good way to do that is increasing them linearly at each half-sweep from the number of states at the end of the infinite algorithm to the number you want to keep at the end.

The rest is just doing a loop for the sweeps, each finite sweep comprising a “half-sweep” to the left and a “half-sweep” to the right, and being sure that during the finite algorithm the size of the system is constant. The implementation (with some extras for saving the results and the rest) looks like this:

def main(args):
    # 
    # create a system object with spin one-half sites and blocks, and set
    # its model to be the TFIM.
    #
    spin_one_half_site = SpinOneHalfSite()
    system = System(spin_one_half_site)
    system.model = HeisenbergModel()
    #
    # read command-line arguments and initialize some stuff
    #
    number_of_sites = int(args['-n'])
    number_of_states_kept = int(args['-m'])
    number_of_sweeps = int(args['-s'])
    number_of_states_infinite_algorithm = 10
    if number_of_states_kept < number_of_states_infinite_algorithm:
	number_of_states_kept = number_of_states_infinite_algorithm
    sizes = []
    energies = []
    entropies = []
    truncation_errors = []
    system.number_of_sites = number_of_sites
    #
    # infinite DMRG algorithm
    #
    max_left_block_size = number_of_sites - 3
    for left_block_size in range(1, max_left_block_size+1):
	energy, entropy, truncation_error = ( 
	    system.infinite_dmrg_step(left_block_size, 
		                      number_of_states_infinite_algorithm) )
	current_size = left_block_size + 3
	sizes.append(left_block_size)
	energies.append(energy)
	entropies.append(entropy)
	truncation_errors.append(truncation_error)
    #
    # finite DMRG algorithm
    #
    states_to_keep = calculate_states_to_keep(number_of_states_infinite_algorithm, 
		                              number_of_states_kept,
		                              number_of_sweeps)
    half_sweep = 0
    while half_sweep < len(states_to_keep):
	# sweep to the left
        for left_block_size in range(max_left_block_size, 0, -1):
	    states = states_to_keep[half_sweep]
            energy, entropy, truncation_error = ( 
                system.finite_dmrg_step('right', left_block_size, states) )
            sizes.append(left_block_size)
            energies.append(energy)
            entropies.append(entropy)
            truncation_errors.append(truncation_error)
	half_sweep += 1
	# sweep to the right
	# if this is the last sweep, stop at the middle
	if half_sweep == 2 * number_of_sweeps - 1:
	    max_left_block_size = number_of_sites / 2 - 1
        for left_block_size in range(1, max_left_block_size + 1):
            energy, entropy, truncation_error = ( 
                system.finite_dmrg_step('left', left_block_size, states) )
            sizes.append(left_block_size)
            energies.append(energy)
            entropies.append(entropy)
            truncation_errors.append(truncation_error)
	half_sweep += 1
    # 
    # save results
    #
    output_file = os.path.join(os.path.abspath(args['--dir']), args['--output'])
    f = open(output_file, 'w')
    zipped = zip (sizes, energies, entropies, truncation_errors)
    f.write('\n'.join('%s %s %s %s' % x for x in zipped))
    f.close()
    print 'Results stored in ' + output_file

See a full implementation of the above code. To learn how to run this code you can use:

$ ./tutorial/solutions/heisenberg.py --help
Implements the full DMRG algorithm for the S=1/2 AF Heisenberg.

Calculates the ground state energy and wavefunction for the
antiferromagnetic Heisenberg model for a chain of spin one-half. The
calculation of the ground state is done using the full DMRG algorithm,
i.e. first the infinite algorithm, and then doing sweeps for convergence
with the finite algorithm.

Usage:
  heisenberg.py (-m=<states> -n=<sites> -s=<sweeps>) [--dir=DIR -o=FILE]
  heisenberg.py -h | --help

  Options:
    -h --help         Shows this screen.
    -n <sites>        Number of sites of the chain.
    -m <states>       Number of states kept.
    -s <sweeps>       Number of sweeps in the finite algorithm.
    -o --output=FILE  Ouput file [default: heisenberg.dat]
    --dir=DIR         Ouput directory [default: ./]

You can use this script to plot the entropies and fit them to the result from conformal field theory.